COORDONNÉES CÉLESTES
Coordonnées Célestes
Francis MICHEL
8 Mars 2017
Les figures viennent de
https://sciencesphysiques.acdijon.fr/astronomie/lexique/lexique_astro/c/coordonnees_celestes.htm
Coordonnées locales :

Les coordonnées locales repèrent les astres par rapport à l'horizon et la hauteur dans le ciel.
Sur l'horizon l'angle (Sm, a) du Sud à la projection verticale de l'astre est l'azimut ; attention, cet angle est parfois mesuré à partir de Nord
Verticalement l'angle (mM, h) de l'horizon à l'astre est la hauteur
La mi-hauteur, 45°, paraît déjà haute quand on regarde le ciel à l'œil nu. Pour un usage courant on remplace l'azimut par les points cardinaux (N,E,S,O) et leurs subdivisions (NE,SE,SO etc.).
Coordonnées horaires

Ces coordonnées se mesurent par rapport à l'équateur céleste et le méridien du lieu. L'équateur céleste est la projection de l'équateur terrestre sur le ciel. Sa perpendiculaire est dirigée vers le pôle Nord tout près de l'étoile Polaire. La hauteur de l'étoile polaire est égale à la latitude du lieu.
L'angle (Em, H) se mesure sur l'équateur céleste à partir du méridien du lieu est l'angle horaire. L'angle horaire du Soleil est nul à midi, ensuite H est le temps solaire vrai. Il servait dans le temps à régler les horloges ; on le corrigeait (équation du temps) ensuite pour avoir le temps solaire moyen.
L'angle (mM, δ) se mesure à partir de l'équateur vers le pôle Nord. Cet angle est indépendant du lieu.
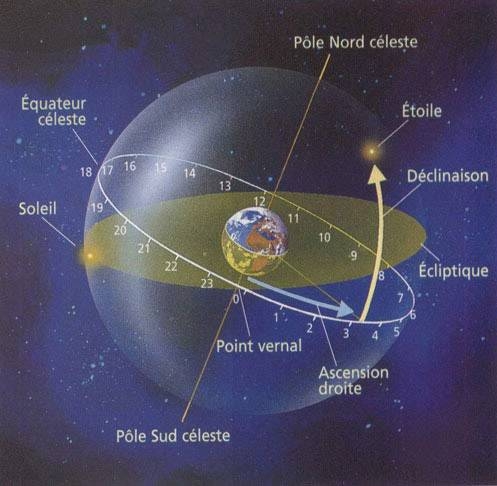
Coordonnées équatoriales :

Ces coordonnées sont indépendantes du lieu. Elles se mesurent par rapport à l'écliptique et l'équateur. L'écliptique est la projection de l'orbite terrestre sur le ciel. Ce cercle fait un angle d'environ 23° avec l'équateur dû à l'inclinaison de l'axe de la Terre. L'intersection de ces deux cercles (γ), du côté du Soleil au printemps, est appelé point vernal.
L'angle (γm, α) se mesure sur l'écliptique à partir du point vernal vers l'Est (sens direct) c'est l'ascension droite. Cette appellation très ancienne faisait référence la hauteur (ascension) verticalement (droite) du Soleil.
L'angle (mM, δ) est la déclinaison comme décrite précédemment.
L'axe de rotation des télescopes est souvent orienté perpendiculairement à l'équateur, l'axe dirigé vers le pôle (monture équatoriale). Cela permet de suivre un astre en ne modifiant qu'un angle avec un moteur synchrone. De plus les coordonnées équatoriales permettent de repérer un astre indépendamment du lieu. Ces coordonnées sont celles qui sont utilisées actuellement pour établir des catalogues d'étoiles et des éphémérides. C'est assez récent, un ou deux siècles, avant on utilisait les coordonnées écliptiques :
Coordonnées écliptiques :

Comme les coordonnées équatoriales ces coordonnées sont indépendantes du lieu. La conversion est aisée (un peu de math).
La longitude (γm, L) se mesure sur l'écliptique à partir du point vernal (γ) vers l'Est
La latitude (mM,λ) se mesure perpendiculairement à l'écliptique
L'intérêt de ces coordonnées c'est que c'est à peu près le chemin des planètes et de la Lune dans le ciel et exactement celui du Soleil.
Les constellations qui sont sur ce cercle est le Zodiaque :